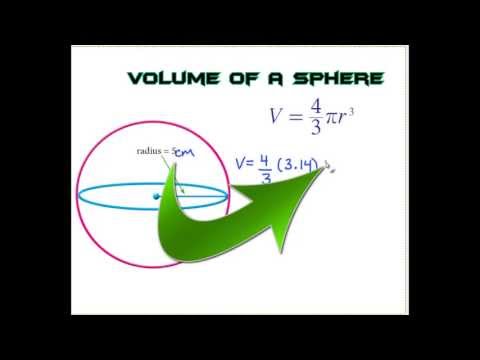
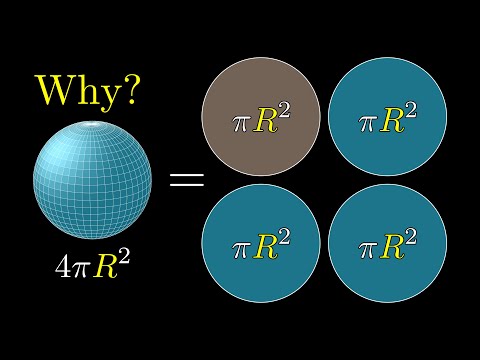A sphere is a three-dimensional, round object, such as a marble or soccer ball. The volume represents the space enclosed by the object. The formula for the volume of a sphere is 4/3 times pi times the radius cubed. Cubing a number means multiplying it by itself three times, in this case, the radius times the radius times the radius. To find the volume in terms of pi, leave pi in the formula rather than converting it to 3.14.
The volume of sphere is the capacity it has. It is the space occupied by the sphere. The volume of sphere is measured in cubic units, such as m3, cm3, in3, etc.
Volume Of A Sphere With Diameter 9 4 Feet The shape of the sphere is round and three-dimensional. It has three axes as x-axis, y-axis and z-axis which defines its shape. All the things like football and basketball are examples of the sphere which have volume. This online calculator will calculate the 3 unknown values of a sphere given any 1 known variable including radius r, surface area A, volume V and circumference C. It will also give the answers for volume, surface area and circumference in terms of PI π. A sphere is a set of points in three dimensional space that are located at an equal distance r from a given point .
The volume of a Sphereis the amount of space contained by a sphere. The volume is calculated by the integration method and measured in cubic units. The volume of a sphere equals four-thirds of the product of \(\pi \) and the cube of the radius. In this lesson, you'll learn how to find the volume of a sphere with a radius of 4 inches.
A sphere is a 3-dimensional round object. The volume is how space is inside the sphere. When you want to find out how much space is inside such a sphere, you'll follow these steps to calculate the volume of the sphere. A simple check on any formula for area or volume is a dimensional check. Area is the two-dimensional amount of space that an object occupies.
Area is measured along the surface of an object and has dimensions of length squared; for example, square feet of material, or square centimeters. Volume is the three-dimensional amount of space that an object occupies. Volume has dimensions of length cubed; for example, cubic feet of material, or cubic centimeters (cc's). One can calculate theweightof any object by multiplying thedensityof the material by the volume of the object.
On this slide, we list some equations for computing the volume of objects which often occur in aerospace. There are similar equations for computing theareaof objects. The magnitude of theaerodynamic forcesdepends on the surface area of an object, while thegravitational forceand certainthermodynamic effectsdepend on the volume of the object. The equations to compute area and volume are used every day by design engineers. A sphere is a three-dimensional solid with no face, no edge, no base and no vertex. It is a round body with all points on its surface equidistant from the center.
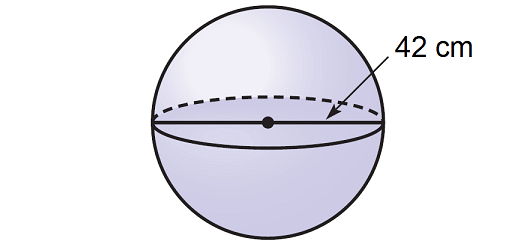
The volume of a sphere is measured in cubic units. A glass dome for a lighting fixture is in the shape of a hemisphere. The circumference of the great circle of the hemisphere is 12π inches.
Which statements about the hemisphere are true? The total surface area is 108π square inches. The total surface area is 144π square inches. The total surface area is 432π square inches. The total surface area is 36π square inches.
For any other value for the length of the radius of a sphere, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the surface area and volume of parts of a sphere. The volume of a sphere is determined by the three coordinates x, y, and z. Because a three-dimensional object will lie on all three axes. Volume is measured in cubic meters, cubic feet, cubic inches, and similar units.
It is represented by symbols cm3, m3, in3, and so on. A sphere is a three-dimensional solid with no base, no edge, no face and no vertex. Sphere is a round body with all points on its surface equidistant from the center. A sphere is the shape of a basketball, like a three-dimensional circle.
Just like a circle, the size of a sphere is determined by its radius, which is the distance from the center of the sphere to any point on its surface. The formulas for the volume and surface area of a sphere are given below. If you ever wondered what's the volume of the Earth, soccer ball or a helium balloon, our sphere volume calculator is here for you.
It can help to calculate the volume of the sphere, given the radius or the circumference. Also, thanks to this calculator you can determine the spherical cap volume or hemisphere volume. This statement is not at all obvious or elementary. "A sphere's volume is two cones of equal height and radius to that of the sphere's".
The assertion about the cone and the cylinder is a little easier to prove, but it too is not obvious. So you have not really provided an answer to this to year old question. I think the accepted answer is closest to what you have in mind.
If you want to help here I think you should pay attention to new questions that don't yet have answers. A sphere with radius R is a three-dimensional geometrical object where the distance between the center and any point on the surface equal to R. Every plane section of a sphere is a circle.
A plane section through the center results in a largest possible circle with radius R. Calculating volume and surface area of sphere play an important role in mathematics and real life as well. Formulas for volume & surface area of sphere can be used to explore many other formulas and mathematical equations.
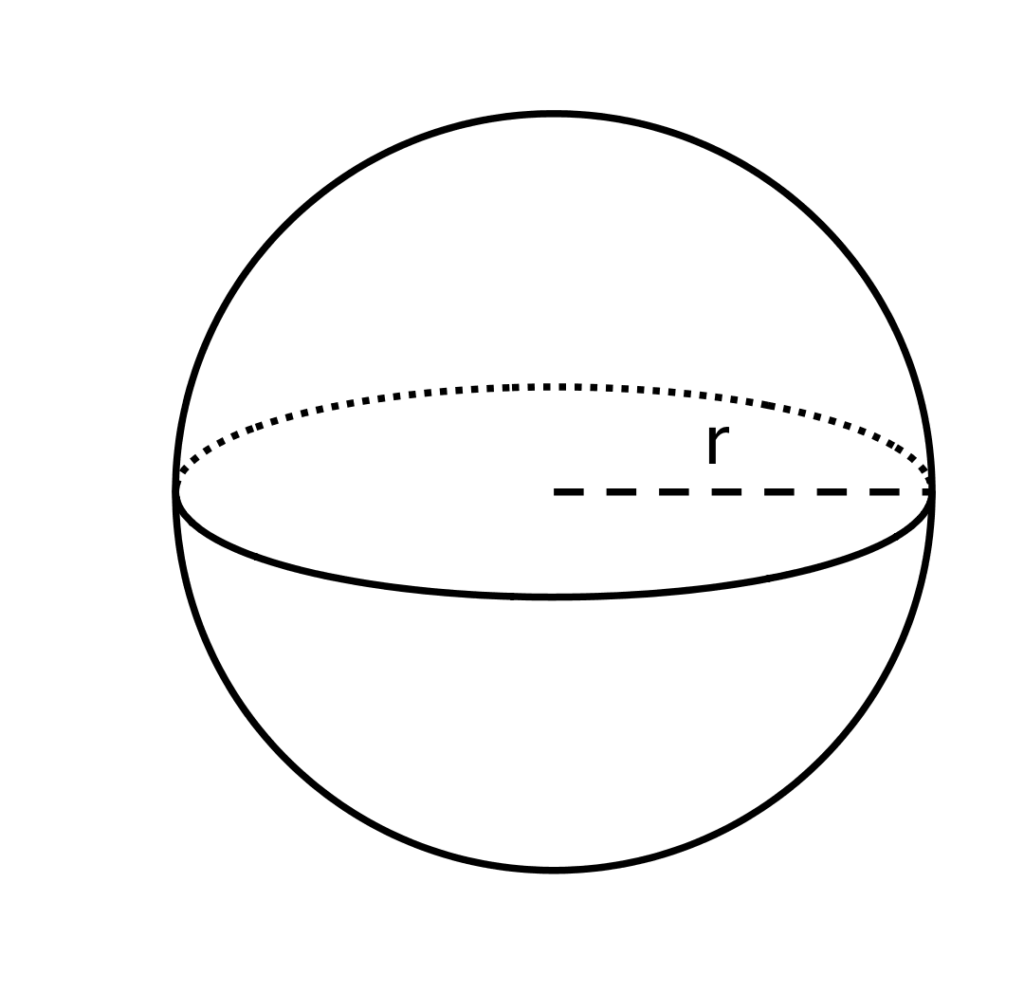
A set of points in a space equally distanced from a given point $O$ is a sphere. The point $O$ is called the center of the sphere. The distance from the center of a sphere to any point on the sphere is called the radius of this sphere. A radius of a sphere must be a positive real number. The segment connecting two points on the sphere and passing through the center is called a diameter of the sphere.
All radii of the sphere are congruent to each other. A sphere can be obtained by rotating a semicircle about the diameter. Two spheres of the same radius are congruent. In this calculation you can calculate the volume of a sphere with a number of given input values, such as radius, diameter, circumference. You also have a number of different input units and can choose output unit according to your likings. The baseball is not regulation size.
If the baseball has a surface area of 9π, then I can set that equal to the formula 4πr2 and solve for r. The radius is 3/2 inches, so I double that to find the diameter. The diameter of the ball is 3 inches, which is greater than the allowed range of diameters. A regulation baseball must have a diameter between 2.87 and 2.94 inches.
The surface area of a particular baseball is 9π square inches. Is the baseball within the range of regulation size? The volume of a sphere formula can be found in terms of the diameter. The diameter of a sphere is the longest line that is inside the sphere and that passes through the center of the sphere. A sphere is a three-dimensional shape that is perfectly symmetrical and round in shape.
Some examples of spheres are a ball, a globe, etc. The volume of a sphere is the amount of space that is inside it the capacity of the sphere that it can hold. In this article, we will derive the diameter of a sphere formula using the volume. Now the question becomes calculating the volume of the bicylinder . It is also very difficult, so add a cube packing the bicylinder . Now when the plane intersects the cube, it forms another larger square.
The extra area in the large square , is the same as 4 small squares . Moving through the whole bicylinder generates a total of 8 pyramids. The inner diameter of a cross section is 4 cm, the outer diameter being 4.4 cm (see Fig. 13.11).
Find its inner curved surface area, outer curved surface area, total surface area. Romm Ă hietal SIOOL A metal pipe is 77 cm long. Find its @ inner curved surface area, (@) outer curved surface area, 3. Find its i) inner curved surface area, outer curved surface area, total surface area ...
Find its 0 inner curved surface area, outer curved surface area, total surface area ... Find its 0 inner curved surface area, 3. Inner curved surface area, () outer curved surface area, total surface area. The following video shows how to solve problems involving the formulas for the surface area and volume of spheres.
The angle between two spheres at a real point of intersection is the dihedral angle determined by the tangent planes to the spheres at that point. Two spheres intersect at the same angle at all points of their circle of intersection. They intersect at right angles if and only if the square of the distance between their centers is equal to the sum of the squares of their radii. Although the radical plane is a real plane, the circle may be imaginary or consist of a single point .
The volume of a 3 -dimensional solid is the amount of space it occupies. Volume is measured in cubic units. Be sure that all of the measurements are in the same unit before computing the volume. Multiply the radius times the radius. For example, if the radius of your sphere equals 19 inches, multiply 19 by 19 to get 361 square inches.
7Given a solid sphere of radius R, remove a cylinder whose central axis goes through the center of the sphere. The volume and surface of solids like rectangular prism, cylinders, pyramids, cones and spheres - online calculator. Archimedes wrote about the problem of dividing a sphere into segments whose volumes are in a given ratio, but did not solve it. Although the Earth is not perfectly spherical, terms borrowed from geography are convenient to apply to the sphere. If a particular point on a sphere is designated as its north pole, its antipodal point is called the south pole. The great circle equidistant to each is then the equator.
Great circles through the poles are called lines of longitude or meridians. A line connecting the two poles may be called the axis of rotation. Small circles on the sphere that are parallel to the equator are lines of latitude.
In geometry unrelated to astronomical bodies, geocentric terminology should be used only for illustration and noted as such, unless there is no chance of misunderstanding. The sphere is a fundamental object in many fields of mathematics. Spheres and nearly-spherical shapes also appear in nature and industry. Bubbles such as soap bubbles take a spherical shape in equilibrium. The Earth is often approximated as a sphere in geography, and the celestial sphere is an important concept in astronomy. Manufactured items including pressure vessels and most curved mirrors and lenses are based on spheres.
Spheres roll smoothly in any direction, so most balls used in sports and toys are spherical, as are ball bearings. Assume that the volume of the sphere is made up of numerous thin circular disks which are arranged one over the other as shown in the figure given above. The circular disks have continuously varying diameters which are placed with the centres collinearly. A thin disk has radius "r" and the thickness "dy" which is located at a distance of y from the x-axis.